JTM V, Etap I
Każde z poniższych zadań warte jest taką samą liczbę punktów. Kolejność zadań nie jest powiązana z ich poziomem trudności.
Zadanie 1
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
Wielomian \(P(x)\) ma miejsce zerowe \(x=-2009\) oraz spełnia równanie \[xP(x+1)+14063=(x+2009)P(x).\] Wyznaczyć \(P(4)\).
Zadanie 2
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
Ciąg \(x_n\) jest dany wzorami \(x_1=\frac{1}{123}\) i \(x_{n+1}=x_n^2+x_n\) dla każdego \(n>1\). Znaleźć część całkowitą liczby\[\frac{1}{x_1+1}+\ldots+\frac{1}{x_{645}+1}.\]
Zadanie 3
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
Ciąg \(g\) jest zadany wzorami:
- \(g_0 = 5,\)
- \(g_1 = B,\)
- \(g_n = g_{n - 1} + g_{n - 2}\;\; \textrm{dla}\ n \geq 2.\)
Wiadomo, że \(g_{11} = 12201\). Wyznaczyć \(B\).
Zadanie 4
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
W trójkącie \(ABC\) odcinki \(BM\), \(CN\) są środkowymi. Obliczyć \(|AC|^2\) wiedząc, że \(|BC| = 5\), \(|BM| = 12\), \(|CN| = 15\).
Zadanie 5
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
Niech \(f(x)=x^{31}+a_{30}x^{30}+\ldots+a_1x+a_0=(x-\alpha_1)\ldots(x-\alpha_{31})\) będzie wielomianem posiadającym \(31\) niezerowych pierwiastków całkowitych \(\alpha_1,\ldots,\alpha_{31}\) (możliwe są powtórzenia), a \(p\) będzie liczbą pierwszą. Dla niezerowej liczby całkowitej \(z\) niech \(\nu_p(z)\) będzie największą taką liczbą naturalną, że \(p^{\nu_p(z)}\) dzieli \(z\). Załóżmy, że:
\(\nu_p(\alpha_{1})=\ldots=\nu_p(\alpha_{4})=1\).
\(\nu_p(\alpha_{5})=\ldots=\nu_p(\alpha_{6})=2\).
\(\nu_p(\alpha_{7})=\ldots=\nu_p(\alpha_{9})=7\).
\(\nu_p(\alpha_{10})=\ldots=\nu_p(\alpha_{13})=8\).
\(\nu_p(\alpha_{14})=\ldots=\nu_p(\alpha_{18})=10\).
\(\nu_p(\alpha_{19})=\ldots=\nu_p(\alpha_{24})=11\).
\(\nu_p(\alpha_{25})=\ldots=\nu_p(\alpha_{31})=15\).
Niech \(A_0=(0,\nu_p(a_0))\) i \(A_{31}=(31,\nu_p(a_{31}))\) będą punktami na płaszczyźnie \(\mathbb{R}^2\). Dla każdego \(1\le i\le 30\) takiego, że \(a_i\ne 0\) i punkt \((i,\nu_p(a_i))\) leży poniżej prostej \(A_0A_{31}\), zaznaczamy ten punkt na płaszczyźnie. Niech \(N\) będzie otoczką wypukłą zaznaczonych punktów. Znaleźć pole \(N\).
Zadanie 6
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
Funkcja \(f:\mathbb{R}\to\mathbb{R}\) spełnia równanie \[11f(x)+16f\left(\frac{x-1}{x+1}\right)=15x+56\] dla każdego \(x\in\mathbb{R}\setminus\{-1\}\). Podać sumę licznika i mianownika ułamka nieskracalnego liczby \(f(17)\) o mianowniku dodatnim.
Zadanie 7
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
Dany jest sześcian zawarty między płaszczyznami \(x = -13\), \(x = 13\), \(y = -13\), \(y = 13\), \(z = -13\), \(z = 13\) kartezjańskiego układu współrzędnych. Z punktu \((0, 0, 0)\) puszczono wiązkę lasera w kierunku punktu \((13, 30, 68)\). Laser idealnie odbija się od ścian sześcianu (promień i promień odbity są symetryczne względem prostej prostopadłej do ściany w punkcie odbicia). Obliczyć kwadrat odległości, jaką pokona wiązka, zanim powróci po raz pierwszy do punktu \((0, 0, 0)\).
Zadanie 8
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
Funkcja \(f:\mathbb{N}_+\to\mathbb{N}_+\) spełnia warunki \(f(1) = 1\), \(f(2n) = f(n)\) oraz \(f(2n + 1) = f(2n) + 1\) dla dowolnej liczby całkowitej \(n\geq 1\). Wyznaczyć maksymalną możliwą wartość \(f(n)\) dla \(1\leq n\leq 9999\).
Zadanie 9
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
Bogdanowo jest położone 21 km dokładnie na zachód od Andrzejowa i 19 km dokładnie na północ od Czesławowa. O 12:00 Celina wyrusza rowerem prostą drogą z Czesławowa do Andrzejowa poruszając się ze stałą prędkością 11 km/h. W tym samym momencie Ania wyrusza rowerem z Andrzejowa do Czesławowa jadąc przez Bogdanowo (porusza się ze stałą prędkością po prostej drodze do Bogdanowa, a następnie po prostej drodze do Czesławowa). Okazało się, że obie dziewczyny dotarły do swoich celów podróży o tej samej godzinie. Znaleźć najmniejszą odległość, jaka dzieliła dziewczyny w linii prostej w trakcie ich podróży. Jako wynik podać całkowitą liczbę metrów otrzymanego wyniku.
Zadanie 10
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
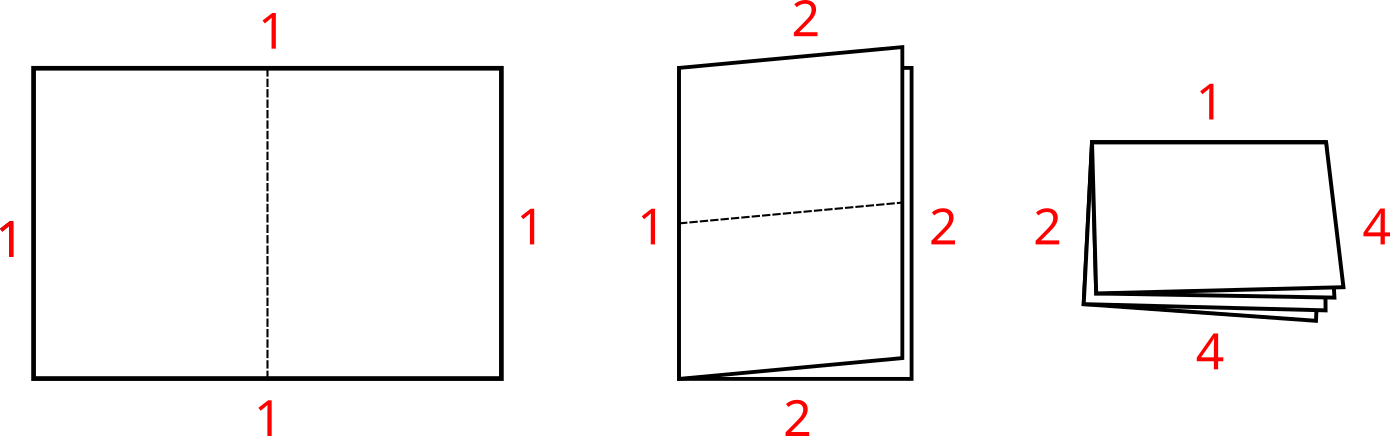
Bartek wziął do ręki prostokątną kartkę papieru o wymiarach \(3\times 2\) i przypisał do każdej krawędzi liczbę \(1\). Następnie \(10\) razy zagiął ją wzdłuż dłuższego boku (patrz rysunek). Po każdym zagięciu liczby na krawędziach kartki są modyfikowane w następujący sposób:
- nowopowstała krawędź będąca grzbietem zagięcia dostaje liczbę 1,
- krawędzie, które zostają złożone w połowie, podwajają swoją liczbę (są zawsze dwie takie),
- ostatnia, czwarta krawędź dostaje liczbę będącą sumą liczb obu krawędzi, które złożyły się razem wzdłuż niej.
Liczby przypisane do poszczgólnych krawędzi po zagięciu zastępują liczby które ewentualnie były przypisane przed zagięciem. Jaka jest suma liczb przypisanych do czterech krawędzi złożonej kartki po 10 zagięciach?
Zadanie 11
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
Zygmunt, Sławomir i Mirosław grają w następującą grę. Jest \(144\) kolejno ponumerowanych pojemników, w których są kulki. Począwszy od Zygmunta gracze kolejno wykonują ruchy polegające na wybraniu pojemnika, a następnie wyjęciu z niego jednej lub więcej kulek. Gracze mogą w każdej chwili sprawdzić liczby kulek w poszczególnych pojemnikach. Przegrywa osoba następująca po osobie, która wzięła ostatnie kulki. Pozostali gracze wygrywają. Ile jest ciągów \((j_1,\ldots,j_{144})\) spełniających następujące warunki:
- na początku rozgrywki w pojemniku o numerze \(i\) znajduje się \(j_i\) kulek;
- \(0\leq j_1\leq\ldots\leq j_{144}\leq 167\);
- Zygmunt może sobie zapewnić wygraną nawet, jeśli Sławomir i Mirosław zmówią się przeciw niemu?
Zadanie 12
Poniżej podana jest przykładowa treść zadania. Treść zadania obowiązująca danego zawodnika dostępna jest po zalogowaniu.
Na ścianie w pokoju Kacpra wisi figura złożona z metalowych drutów (rysunek pokazuje figurę poziomu 4-tego, czyli 4 prostokąty w środkowej pionowej kolumnie). Kacper chce wykonać jej dokładną kopię. W tym celu przygotował pojedynczy kawałek drutu długości równej dokładnie sumie długości drutów figury na ścianie. Zamierza go pociąć na kawałki, które pozagina i zespawa ze sobą. Na ile co najmniej kawałków będzie musiał rozciąć ten drut, aby po ich zagięciu i zespawaniu otrzymać figurę poziomu \(127\)?