JTM I, Etap IIIA
Każde z poniższych zadań warte było 1 punkt. Kolejność zadań nie jest powiązana z ich poziomem trudności.
Zadanie 1
Na potrzeby tego zadania przyjmijmy następujące nazewnictwo:
- pisząc ,,kilka'', mamy na myśli liczbę naturalną ze zbioru \(\{2,...,9\}\);
- pisząc ,,kilkanaście'', mamy na myśli liczbę naturalną ze zbioru \(\{11,...,19\}\);
- pisząc ,,kilkadziesiąt'', mamy na myśli liczbę naturalną ze zbioru \(\{50,...,99\}\);
- pisząc ,,kilkaset'', mamy na myśli liczbę naturalną ze zbioru \(\{500,...,999\}\).
Zadanie 2
Na planie architektonicznym pewnego budynku podstawa jego dachu jest wyznaczona nierównościami \(|10x+2y+7|\leq 45\) oraz \(-10\leq 2y+2\leq 13-x\). Wysokość punktu tego dachu o współrzędnych \((x,y)\) na tym planie wyrażona w decymetrach przedstawia się wzorem \(h=|x-1|-|y+1|-2x+3y+35\). Wyznaczyć wysokość wyrażoną w decymetrach najwyższego punktu dachu.
Zadanie 3
Niech \(S\) oznacza najmniejszą wartość funkcji \(f:\left (0, \frac{\pi}{2} \right ) \to \mathbb{R}\) danej jako
\[f(x) = \left ( \frac{1}{9} + \frac{32}{\sin x} \right )\left ( \frac{1}{32} + \frac{9}{\cos x} \right ).\]
Wyznaczyć część całkowitą liczby \(S\).
Zadanie 4
Liczbę naturalną dodatnią nazwiemy dziwną, jeśli posiada dzielnik pierwszy większy od jej pierwiastka kwadratowego. Ile jest dziwnych liczb naturalnych dodatnich, których wszystkie dzielniki pierwsze są mniejsze od \(40\)?
Zadanie 5
Kwadratowy arkusz papieru w kratkę podzielony jest na \(2^{12}\) kwadracików ponumerowanych liczbami \(1\), \(2\), \(3\), ..., \(2^{12}-1\), \(2^{12}\) rzędami, jak na rysunku.
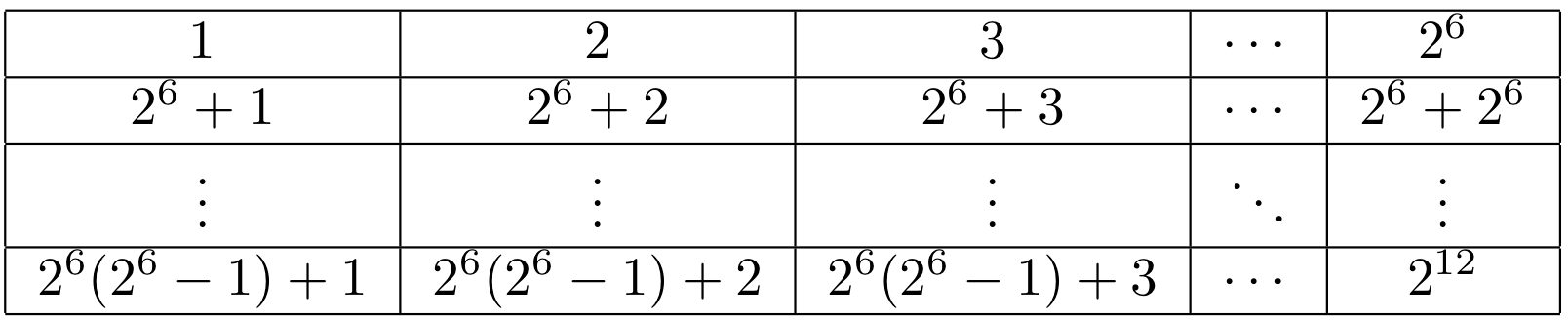
Akcją L nazwiemy przecięcie arkusza dokładnie w połowie w pionie i pozostawieniu lewej części. Analogicznie zdefiniujmy akcje P, G, D, które oznaczać będą odpowiednio przecięcia: w pionie i pozostawienie prawej części, w poziomie i pozostawienie górnej części oraz w poziomie i pozostawienie dolnej części. Po wykonaniu \(12\) takich akcji pozostanie jeden kwadracik. Na ile sposobów, wykonując akcje L, P, G, D, możemy otrzymać kwadracik o numerze \(2017\)?
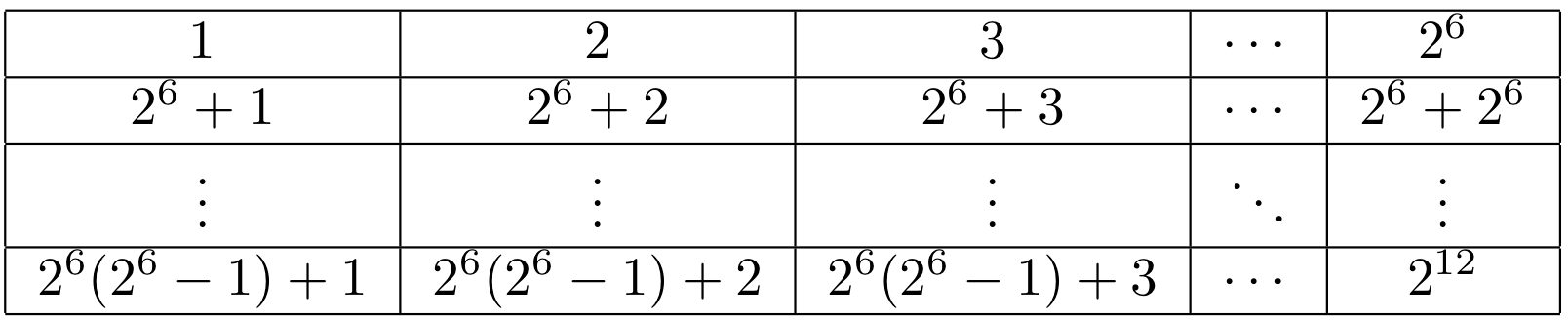
Akcją L nazwiemy przecięcie arkusza dokładnie w połowie w pionie i pozostawieniu lewej części. Analogicznie zdefiniujmy akcje P, G, D, które oznaczać będą odpowiednio przecięcia: w pionie i pozostawienie prawej części, w poziomie i pozostawienie górnej części oraz w poziomie i pozostawienie dolnej części. Po wykonaniu \(12\) takich akcji pozostanie jeden kwadracik. Na ile sposobów, wykonując akcje L, P, G, D, możemy otrzymać kwadracik o numerze \(2017\)?
Zadanie 6
W trójkącie \(ABC\) kąt \(CAB\) ma miarę \(120^{\circ}\), zaś kąt \(BCA\) \(180^{\circ}-2\alpha\). Punkt \(M\) został tak wybrany na odcinku \(BC\), że kąty \(CAM\) i \(AMC\) mają miarę \(\alpha\). Wiedząc, że \(\tan\alpha=5\sqrt{3}\), podać licznik ilorazu \(\frac{|BM|}{|AB|}\) zapisanego w postaci ułamka nieskracalnego o dodatnim mianowniku.
Zadanie 7
Wielomian piątego stopnia \(W\) ma współczynnik wiodący równy \(-7\). Ponadto \(W(1)=-2\), \(W(2)=-4\), \(W(3)=-6\), \(W(4)=-8\), \(W(5)=-10\). Ile wynosi współczynnik wolny wielomianu \(W\)?
Zadanie 8
Jaś gra w następującą grę. Rzuca symetryczną sześcienną kostką, a wyrzuconą liczbę oczek zapisuje na kartce. Ponadto, za każdym razem, gdy wyrzuci jedno lub dwa oczka, to rzuca kostką jeszcze raz. W przeciwnym przypadku przestaje rzucać kostką. Dla przykładu, jeśli Jaś wyrzuci jedno oczko, to zapisuje na kartce liczbę \(1\) i rzuca jeszcze raz. Jeśli za drugim razem wyrzuci cztery oczka, to zapisuje na kartce liczbę \(4\) i kończy grę. Po zakończeniu gry Jaś dodaje do siebie zapisane liczby. W powyższym przykładzie otrzyma więc sumę \(1+4=5\). Obliczyć prawdopodobieństwo zdarzenia, że suma wyrzuconych przez Jasia oczek wyniesie \(4\). Wynik podać w postaci ułamka nieskracalnego o dodatnim mianowniku.
Zadanie 9
Znaleźć sumę długości krawędzi czworościanu wiedząc, że istnieje kula styczna do wszystkich jego krawędzi oraz długości pewnych jego krawędzi skośnych to \(3\) i \(5\).
Zadanie 10
Niech \(f:\mathbb{R}\setminus\{0,1\}\rightarrow\mathbb{R}\) będzie funkcją spełniającą równość
\[f\left(\frac{1}{1-x}\right)+2f\left(\frac{x-1}{x}\right)=3x\]
dla dowolnej liczby rzeczywistej \(x\in\mathbb{R}\setminus\{0,1\}\). Podać wartość \(f(-1)\).





