JTM I, Etap IIIB
Każde z poniższych zadań warte było 0.5 punktu. Kolejność zadań nie jest powiązana z ich poziomem trudności. Autorem wszystkich zadań jest dr Krzysztof Ciesielski.
 |
|
Wykład dra Ciesielskiego poprzedzający drugą część testu. Cała galeria z finału: [link] |
Zadanie 1
Podać ostatnią cyfrę liczby \(8102^{2018}\).
Zadanie 2
Ile jest różnych liczb pięciocyfrowych, które można ułożyć
mając do dyspozycji cyfry 0,1,2,3,4 (żadna z cyfr nie może się
powtórzyć)?
Zadanie 3
Przy dzieleniu liczby 1997 przez pewną liczbę trzycyfrową \(n\)
otrzymano resztę 2. Jaka jest reszta przy dzieleniu 6005 przez tę
samą liczbę \(n\)?
Zadanie 4
Miary kątów w trójkącie mają się do siebie jak 1:5:6. Najdłuższy
bok trójkąta wynosi 20. Ile wynosi wysokość opuszczona na ten bok?
Zadanie 5
Kolorowe kartki pakowane są w paczkach po 500 sztuk.
Zdjęcie paczki z półki zajmuje sprzedawcy 10 sekund, wyjęcie jednej
kartki z paczki -- sekundę (niezależnie od tego, czy wyjmuje po
jednej kopercie, czy odlicza odpowiednią liczbę i wyjmuje razem).
Klient poprosił o 100 kartek czerwonych, 50 niebieskich, 100 żółtych
i 450 fioletowych. Na półkach są w tym momencie wyłącznie pełne
paczki. W jakim najkrótszym czasie sprzedawca może mu wręczyć
kartki? Należy podać liczbę w sekundach.
Zadanie 6
Ile zer ma na końcu liczba 1000! ?
Zadanie 7
Niektóre z jedenastu dużych pudełek zawierają po 8 średnich
pudełek, niektóre spośród średnich pudełek zawierają po 8 małych
pudełek. Okazało się, że 102 pudełka są puste. Jaka jest łączna
liczba pudełek?
Zadanie 8
Ile wynosi promień okręgu wpisanego w wycinek koła o promieniu
6 i kącie \(60^{\circ}\) (rysunek)?
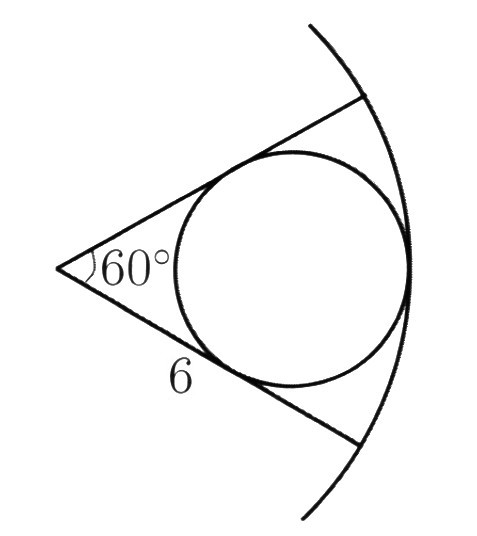

Zadanie 9
Ile dzielników mniejszych od \(10000\) ma liczba \(15840\)?
Zadanie 10
Liczba \(17!\) zapisana w systemie dziesiętnym ma postać
\(35568x428096y00\), przy czym \(x\) i \(y\) są cyframi. Ile wynosi
\(x\)?
Zadanie 11
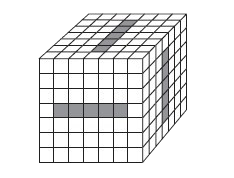
Sześcian zbudowany jest z \(7^3\) małych, identycznych kostek
sześciennych. Usuwamy z niego część sześcianików, drążąc trzy
wzajemnie prostopadłe tunele o szerokości pięciu kostek w
prostopadłych ścianach tak, jak na rysunku. Ile małych kostek
pozostało?

Zadanie 12
Na półce z książkami stoi 10 tomów encyklopedii. Kornik
książkowy, który wystartował z pierwszej strony pierwszego tomu,
przegryza jedną tekturową stronę okładki przez 3 godziny, a
wszystkie kartki dowolnego z tomów przez 2 godziny. Po jakim czasie
dotrze do ostatniej strony tomu dziesiątego?
Zadanie 13
Iloczyn liczb wieku dzieci pana Jana wynosi 1664. Najstarsze
dziecko jest 2 razy starsze od najmłodszego. Ile wynosi suma lat
wszystkich dzieci pana Jana?
Zadanie 14
Ile zer ma na końcu iloczyn kolejnych 2018 początkowych liczb
pierwszych?
Zadanie 15
Sześcian o wymiarach \(5 \times 5 \times 5\) został zbudowany
przez sklejenie ze sobą 125 identycznych kostek jednostkowych.
Kładziemy sześcian na podłodze. Ile maksymalnie kostek
jednostkowych możemy zobaczyć?
Zadanie 16
Ile wynosi suma współczynników wielomianu danego wzorem
\(W(x) = (x^2 + x - 3)^{2018} - (x^3 - x^2 + x - 1)^{555} + (3x^2 + x
+ 3)^{2}\)?
Zadanie 17
Ile wynosi \(\sqrt{7 \cdot 8^4 - 7 \cdot 6^4}\)?
Zadanie 18
Ile płaszczyzn symetrii ma sześcian?





